Bernoulli process

\begin{align}
{\rm{P}}\left( {{\rm{sucess}}} \right) &= {\rm{P}}\left( {{X_i} = 1} \right) = p\\
{\rm{P}}\left( {{\rm{failure}}} \right) &= {\rm{P}}\left( {{X_i} = 0} \right) = 1 – p\\
{\rm{E}}\left[ {{X_t}} \right] &= p,{\mathop{\rm var}} \left( {{X_t}} \right) = p\left( {1 – p} \right)
\end{align}

PMF of # of arrivals (number of success \(S\) in \(n\) time slots): binomial pmf

\begin{align}
{\rm{P}}\left( {S = k} \right) &= \left( \begin{array}{l}
n\\
k
\end{array} \right){p^k}{\left( {1 – p} \right)^{n – k}}, \ k = 0,1, \cdots ,n\\
{\rm{E}}\left[ S \right] &= np\\
{\mathop{\rm var}} \left( S \right) &= np\left( {1 – p} \right)
\end{align}

Interarrival time distribution: geometric pmf

\begin{align}
{\rm{P}}\left( {{Y_k} = t} \right) &= {\left( {1 – p} \right)^{t – 1}}p, \ t = 1,2, \cdots \\
{\rm{E}}\left[ {{Y_k}} \right] &= 1/p\\
{\mathop{\rm var}} \left( {{Y_k}} \right) &= \left( {1 – p} \right)/{p^2}
\end{align}

Time to \(k\)th arrival: Pascal pmf

\begin{align}
{Y_k} &= {T_1} + {T_2} + \cdots + {T_k},{T_i} \sim {\rm{geom}}\left( p \right)\\
{{\rm{P}}_{{Y_k}}}\left( t \right) &{\rm{ = P}}\left( {{Y_k} = t} \right) = {\rm{P}}\left( {k – 1 \ {\rm{arrivals \ in}}\left[ {1, \cdots t – 1} \right],{\rm{arrival \ at \ time}} \ t} \right)\\
&= \left( \begin{array}{l}
t – 1\\
k – 1
\end{array} \right){p^{k – 1}}{\left( {1 – p} \right)^{t – k}}p,t \ge k\\
{\rm{E}}\left[ {{Y_k}} \right] &= k/p\\
{\mathop{\rm var}} \left( {{Y_k}} \right) &= k\left( {1 – p} \right)/{p^2}
\end{align}

Poisson process

\[{\rm{P}}\left( {k,\tau } \right) = {\rm{Probability \ of}} \ k \ {\rm{arrivals \ in \ interval \ of \ duration}} \ \tau \]

Small interval probabilities:

\[{\rm{P}}\left( {k,\delta } \right) = \left\{ \begin{array}{l}
1 – \lambda \delta \qquad k = 0\\
\lambda \delta \qquad \quad k = 1\\
0 \qquad \quad k > 1
\end{array} \right.\]

\(\lambda \): arrival rate \({\rm{ = E}}\left[ {{\rm{number \ of \ arrivals}}} \right]/{\rm{unit \ time}}\)

Discretize time into \(n\) time slots, \(n = \frac{\tau }{\delta }\), the probability \(p = \lambda \delta = \frac{{\lambda \tau }}{n}\)

\[{\rm{P}}\left( {k \ {\rm{arrivals \ in \ time}}\ \tau } \right) = \left( \begin{array}{l}
n\\
k
\end{array} \right){\left( {\frac{{\lambda \tau }}{n}} \right)^k}{\left( {1 – \frac{{\lambda \tau }}{n}} \right)^{n – k}}\]

When \(\delta \to 0, \ n \to \infty \), we get Poisson process

\begin{align}
{\rm{P}}\left( {k,\tau } \right) &= \frac{{{{\left( {\lambda \tau } \right)}^k}{e^{ – \lambda \tau }}}}{{k!}},k = 0,1, \cdots ,n\\
{\rm{E}}\left[ {{N_t}} \right] &= \lambda t, \ {\mathop{\rm var}} \left( {{N_t}} \right) = \lambda t
\end{align}

Time of the \(k\)th arrival: Erlang

\begin{align}
{f_{{Y_k}}}\left( t \right)\delta &= {\rm{P}}\left( {t \le {Y_k} \le t + \delta } \right) = {\rm{P}}\left( {k – 1{\rm{arrivalsin}}\left[ {0,t} \right]} \right) \cdot \lambda \delta \\
&= \frac{{{{\left( {\lambda \tau } \right)}^{k – 1}}{e^{ – \lambda \tau }}}}{{\left( {k – 1} \right)!}}\lambda \delta = \frac{{{\lambda ^k}{\tau ^{k – 1}}{e^{ – \lambda \tau }}}}{{\left( {k – 1} \right)!}}\delta
\end{align}

\[{f_{{Y_k}}}\left( y \right) = \frac{{{\lambda ^k}{y ^{k – 1}}{e^{ – \lambda y }}}}{{\left( {k – 1} \right)!}} \qquad {\rm{Erlang \ distribution}}\]

Interarrival times \(k=1\): exponential

\begin{align}
{f_{{T_1}}}\left( t \right) &= \lambda {e^{ – \lambda t}}, \ t \ge 0\\
{\rm{E}}\left[ {{T_1}} \right] &= 1/\lambda
\end{align}

Example: Poisson fishing

Assume one can catch fish at a rate of \(\lambda = 0.6/{\rm{hour}}\). One fishes for two hours and continue until the first catch if there is no catch in the first two hours.

\begin{align}
{\rm{P}}\left( {{\rm{fish \ time}}>2} \right) &= {\rm{P}}\left( {0,2} \right) = \frac{{{{\left( {\lambda \tau } \right)}^0}}}{{0!}}{e^{ – 0.6 \cdot 2}} = {e^{ – 1.2}}\\
&={\rm{P}}\left( {{T_1} \ge 0.2} \right) = \int_2^\infty {{f_{{T_1}}}\left( t \right)} dt = \int_2^\infty {0.6{e^{ – 0.6t}}} dt = {e^{ – 1.2}}\end{align}

\begin{align}
{\rm{P}}\left( 2 \le  {\rm{fish \ time }} \le 5 \right) &= {\rm{P}}\left( {{\rm{first \ catch \ within}}\left[ {2,5} \right]} \right)\\
&= \int_2^5 {{f_{{T_1}}}\left( t \right)} dt = \int_2^5 {0.6{e^{ – 0.6t}}} dt = {e^{ – 1.2}} – {e^{ – 3}}\\
&= {\rm{P}}\left( {0,2} \right)\left[ {1 – {\rm{P}}\left( {0,3} \right)} \right] = {e^{ – 0.6 \cdot 2}}\left( {1 – {e^{ – 0.6 \cdot 3}}} \right) = {e^{ – 1.2}} – {e^{ – 3}}\end{align}

\begin{align}
{\rm{P}}\left( {{\rm{catch \ at \ least \ }}2 \ {\rm{fish}}} \right) &= {\rm{P}}\left( {{\rm{catch \ at \ least \ }}2{\rm{\ fish \ in}}\left[ {0,2} \right], \ {\rm{otherwise \ go \ home \ until}}1} \right)\\
&= \sum\limits_{k = 2}^\infty {{\rm{P}}\left( {k,2} \right)} = 1 – {\rm{P}}\left( {0,2} \right) – {\rm{P}}\left( {1,2} \right) = 1 – 2.2{e^{ – 1.2}}\\
&= {\rm{P}}\left( {{\rm{the}}\ 2{ \ \rm{fish \ occur \ in}}\left[ {0,2} \right]} \right) = {\rm{P}}\left( {{Y_2} \le 2} \right) \\ &= \int_0^2 {{f_{{T_2}}}\left( t \right)} dt = \int_0^2 {{{0.6}^2}t{e^{ – 0.6t}}} dt = 1 – 2.2{e^{ – 1.2}}\end{align}

\begin{align}
{\rm{E}}\left[ {{\rm{number \ of \ fish}}} \right] &= {\rm{E}}\left[ {{\rm{number \ of \ fish \ caught \ in\ }}\left[ {0,2} \right]} \right]{\rm{ + E}}\left[ {{\rm{number \ of \ fish \ caught \ in \ }}\left[ {2,\infty } \right]} \right]\\
&= \lambda t + \left\{ \begin{array}{l}
1 \ catch \ no \ fish \ during\left[ {0,2} \right]\\
0 \ catch \ at \ least \ 1 \ fish \ during\left[ {0,2} \right]
\end{array} \right. \\ &= \lambda t + {e^{ – \lambda t}}{\rm{P}}\left( {0,2} \right) = 1.2 + {e^{ – 1.2}} \cdot 0.6 \cdot 2{e^{ – 0.6 \cdot 2}}\end{align}

\begin{align}
{\rm{E}}\left[ {{\rm{total \ fishing \ time}}} \right] &= 2 + {\rm{P}}\left( {0,2} \right)\frac{1}{\lambda } = 2 + {e^{ – 1.2}}/0.6
\end{align}

\[{\rm{E}}\left[ {{\rm{future \ fishing \ time}}\left| {{\rm{fished \ for}} \ 4 \ {\rm{hours}}} \right.} \right] = \frac{1}{\lambda } = 1/0.6 \leftarrow {\rm{independent}}\]

Merging Poisson processes

Each light bulb has independent exponential(\(\lambda\)) lifetime. Install three light bulbs and find expected time until last light bulb dies out.

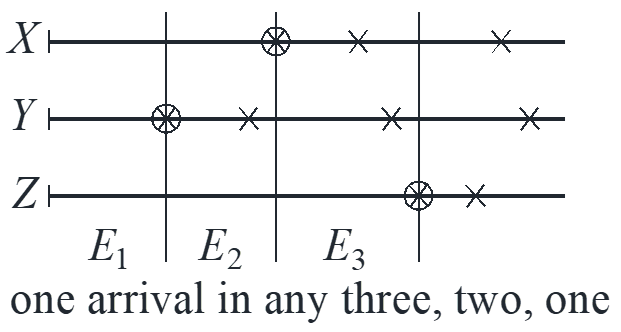
\[{\rm{E}}\left[ {\max \left( {X,Y,Z} \right)} \right] = {{\rm{E}}_1} + {{\rm{E}}_2}{\rm{ + }}{{\rm{E}}_3} = \frac{1}{{3\lambda }} + \frac{1}{{2\lambda }} + \frac{1}{\lambda }\]

Random incidence

Bus interarrival times are equally likely to be 5 or 10 minutes. If you arrive at a random time, what is the expected time to next arrival?

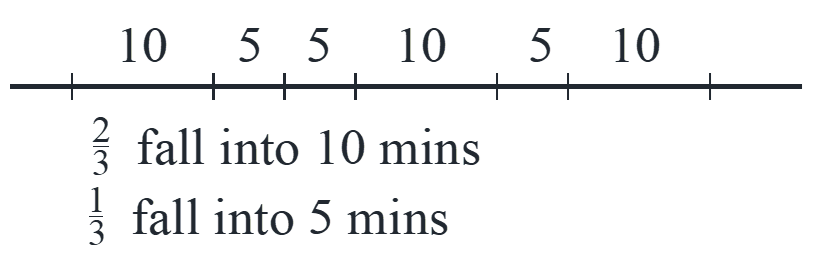
\[{\rm{E}}\left[ T \right] = \frac{2}{3} \cdot 10 + \frac{1}{3} \cdot 5 = \frac{{25}}{3} \ne \frac{{5 + 10}}{2} = 7.5\]

We get biased longer intervals. What we should choose to evaluate the interarrival time of a bus is the random bus rather than random time. There is no contradictory in the claim “family size is 4 on average, but on the average, typical people live in families of 6” because we pick families in the first half and pick person in the second half, and people in large families are more likely to be selected.

Markov chains

Markov assumption: given current state, the past does not matter

\[{{\rm{P}}_{ij}} = {\rm{P}}\left( {{X_{n + 1}} = j\left| {{X_n} = i} \right.} \right) = {\rm{P}}\left( {{X_{n + 1}} = j\left| {{X_n} = i,{X_{n – 1}}, \cdots ,{X_0}} \right.} \right)\]

Recurrent: starting from state \(i\), there is always a way of returning to  state \(i\), otherwise is called transient.

\(n\)-step transition probabilities

\[{r_{ij}}\left( n \right) = {\rm{P}}\left( {{X_n} = j\left| {{X_0} = i} \right.} \right) = \sum\limits_{k = 1}^m {{r_{ik}}\left( {n – 1} \right){p_{kj}}} \]

Steady-state

Yes. if 1.recurrent state are all in a single class, 2.single recurrent class is not periodic.

Take the limit of key recursion as \(n \to \infty \),

\[{r_{ij}}\left( n \right) = \sum\limits_{k = 1}^m {{r_{ik}}\left( {n – 1} \right){p_{kj}}} \to {\pi _j} = \sum\limits_k {{\pi _k}{p_{kj}}} \]

frequency of being in \(j\): \({\pi _j}\)

frequency of transitions \(k \to j\): \({{\pi _k}{p_{kj}}}\)

frequency of transitions into \(j\): \(\sum\limits_k {{\pi _k}{p_{kj}}} \)

Birth-death processes

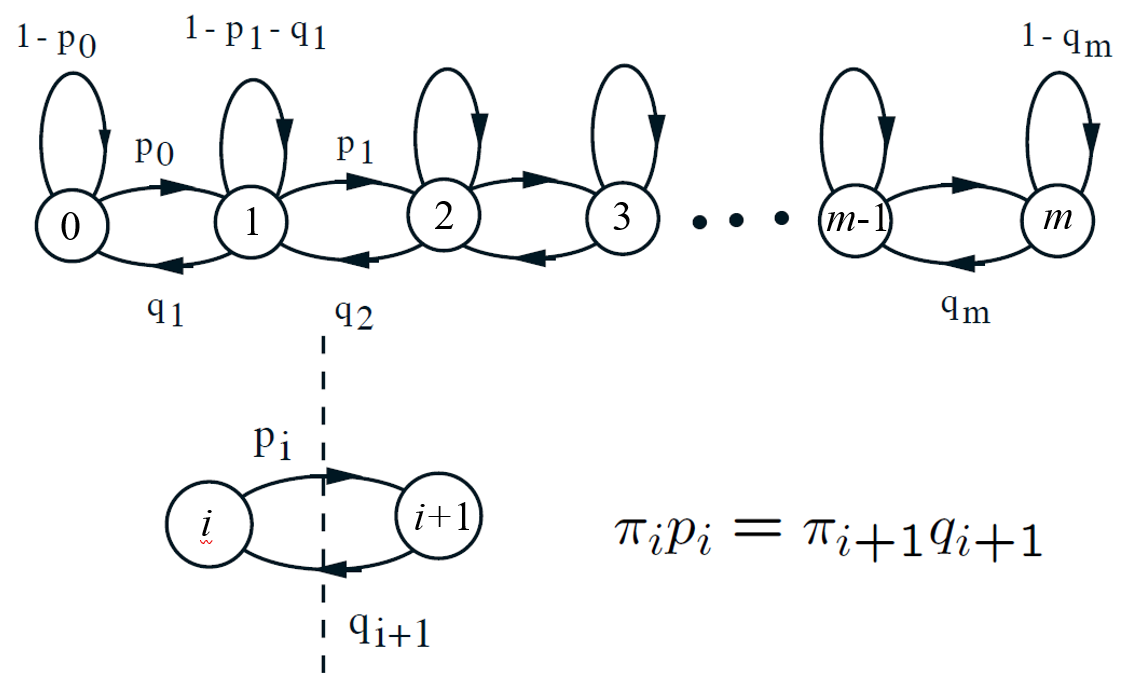
special case: \(p_i=p\) and \(q+i=q\) for all, \(\rho =p/q=\rm{load \ factor}\)

\[{\pi _i} = {\pi _{i – 1}}\rho = {\pi _0}{\rho ^i},i = 0,1, \cdots ,m\]

\begin{align}
p = q,\rho = 1 &\to {\pi _0} = \frac{1}{{m + 1}},{\rm{E}}\left[ {{X_n}} \right] \approx \infty \\
p < q,m \approx \infty &\to {\pi _0} = 1 – \rho ,{\rm{E}}\left[ {{X_n}} \right] = \frac{\rho }{{1 – \rho }}
\end{align}

Phone company problem

Calls originate as a Poisson process at a rate of \(\lambda \). Each call duration is exponentially distributed with parameter \(\mu \) and totally \(B\) lines are available. Find the \(B\) to satisfy \({\pi _B} = {\rm{P}}\left( {{\rm{busy}}} \right)\) is small.

Absorption probabilities

Probability that settle eventually in state 4 given that the initial state is \(i\).

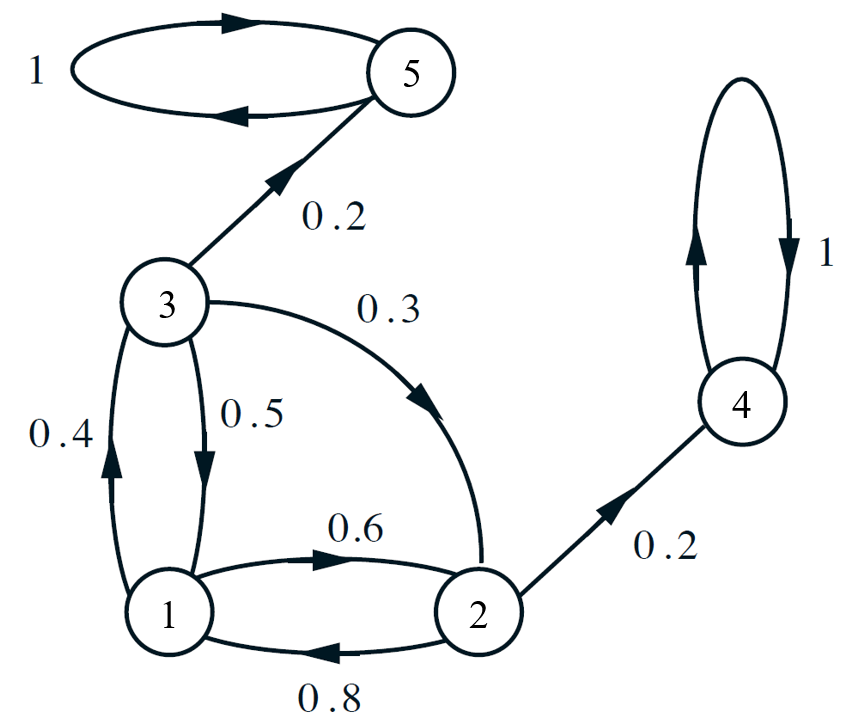
\[\begin{array}{l}
i = 4,{a_4} = 1\\
i = 5,{a_5} = 0
\end{array}\]

\[\left\{ \begin{array}{l}
{a_2} = 0.2 + 0.8{a_1}\\
{a_1} = 0.4{a_3} + 0.6{a_2}\\
{a_3} = 0.3{a_2} + 0.5{a_1}
\end{array} \right. \to {\rm{unique \ solution}}\]

Expected time to absorption

\[\left\{ \begin{array}{l}
{\mu _i} = 0\\
{\mu _i} = 1 + \sum\limits_j {{p_{ij}}{\mu _j}} \qquad {\rm{all \ other}}i
\end{array} \right.\]

Similar to the absorption probability, but we need one step to get to the second step state \(j\). This is the same problem with “how long from state \(i\) to state \(s\) for the first time. We can just remove the arrow from \(s\) to other states because we do not care about what happens after \(s\).