Independent and disjoint

Two events are independent or disjoint are two different concept. If two events are independent, there is no relation between but they can happen together. It is noted that independence can be affected by conditioning. If two events are disjoint, they has the relation that when one happens the other cannot happen and they are not independent.

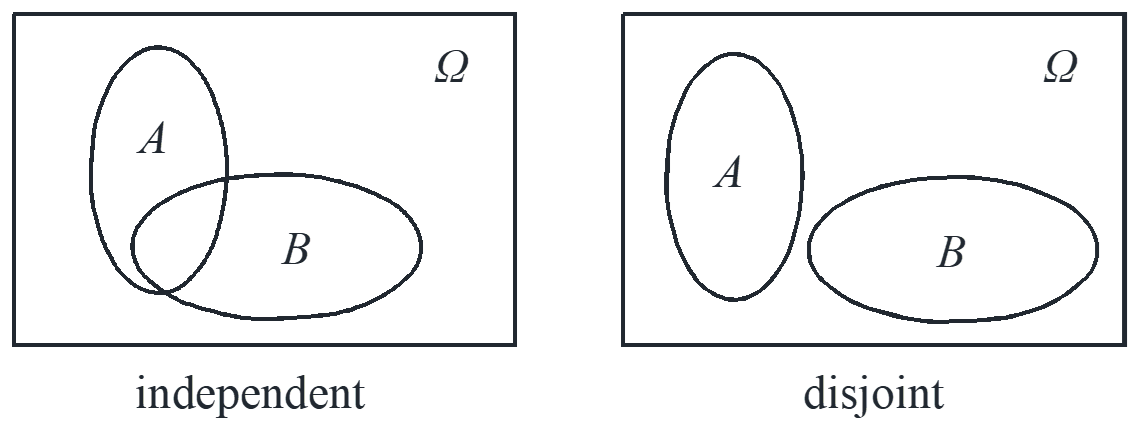
Independent: \({\rm{P}}\left( {B\left| A \right.} \right) = {\rm{P}}\left( B \right) \Leftrightarrow {\rm{P}}\left( {A\left| B \right.} \right) = {\rm{P}}\left( A \right)\)

Disjoint: \({\rm{P}}\left( {A \cap B} \right) = 0 \Leftrightarrow A \cap B = \emptyset \)

Discrete random variables

Multiplication rule: \({\rm{P}}\left( {A \cap B} \right) = {\rm{P}}\left( {\rm{P}} \right){\rm{P}}\left( {A\left| B \right.} \right) = {\rm{P}}\left( A \right){\rm{P}}\left( {B\left| A \right.} \right)\)

Total probability theorem: \(B\) is consist of \({A_1},{A_2},\cdots ,{A_i}\)

\[{\rm{P}}\left( B \right) = \sum {{\rm{P}}\left( {{A_i}} \right){\rm{P}}\left( {{A_i}\left| B \right.} \right)} \]

Bayes’ rule

\[{\rm{P}}\left( {{A_i}\left| B \right.} \right) = \frac{{{\rm{P}}\left( {{A_i} \cap B} \right)}}{{{\rm{P}}\left( B \right)}} = \frac{{{\rm{P}}\left( {{A_i} \cap B} \right)}}{{\sum {{\rm{P}}\left( {{A_i}} \right){\rm{P}}\left( {{A_i}\left| B \right.} \right)} }}\]

PMF: Probability mass function

\begin{align*}
{p_X}\left( x \right) &= {\rm{P}}\left( {X = x} \right) = \sum\limits_y {{p_{X,Y}}\left( {x,y} \right)} \\
{p_{X,Y}}\left( {x,y} \right) &= {\rm{P}}\left( {X = x,Y = y} \right)
\end{align*}

\begin{align*}
{p_{X\left| Y \right.}}\left( {x\left| y \right.} \right) &= {\rm{P}}\left( {X = x\left| {Y = y} \right.} \right) = \frac{{{p_{X,Y}}\left( {x,y} \right)}}{{{p_Y}\left( y \right)}}\\
{p_{X,Y}}\left( {x,y} \right) &= {p_Y}\left( y \right){p_{X\left| Y \right.}}\left( {x\left| y \right.} \right) = {p_X}\left( x \right){p_{Y\left| X \right.}}\left( {y\left| x \right.} \right)
\end{align*}

Expectation

\begin{align*}
{\rm{E}}\left[ X \right] &= \sum\limits_x {x{p_X}\left( x \right)} {\rm{,}}\\
{\rm{E}}\left[ {g\left( X \right)} \right] &= \sum\limits_x {g\left( x \right){p_X}\left( x \right)} \\
{\rm{E}}\left[ {g\left( {X,Y} \right)} \right] v&= \sum\limits_x {\sum\limits_y {g\left( {x,y} \right){p_{X,Y}}\left( {x,y} \right)} }
\end{align*}

\begin{align*}
{\rm{in \ general \ E}}\left[ {g\left( {X,Y} \right)} \right] &\ne g\left( {{\rm{E}}\left[ X \right],{\rm{E}}\left[ Y \right]} \right)\\
g\left( x \right){\rm{is \ linear}} \to {\rm{E}}\left[ {g\left( X \right)} \right] &= g\left( {{\rm{E}}\left[ X \right]} \right)\\
{\rm{E}}\left[ {\alpha X + \beta } \right] &= \alpha {\rm{E}}\left[ X \right] + \beta \\
{\rm{E}}\left[ {x – {\rm{E}}\left[ X \right]} \right] &= {\rm{E}}\left[ X \right] – E\left[ X \right] = 0
\end{align*}

\begin{align*}
{\rm{independent}} \to &{\rm{E}}\left[ {XY} \right] = {\rm{E}}\left[ X \right]{\rm{E}}\left[ Y \right]\\
&{\rm{E}}\left[ {g\left( X \right),h\left( Y \right)} \right] = {\rm{E}}\left[ {g\left( X \right)} \right]{\rm{E}}\left[ {h\left( Y \right)} \right]
\end{align*}

Variance: \({\rm var} \left( X \right) = {\rm{E}}\left[ {{{\left( {X – {\rm{E}}\left[ X \right]} \right)}^2}} \right]\)

\[{\rm var} \left( X \right) = {\rm{E}}\left[ {{{\left( {X – {\rm{E}}\left[ X \right]} \right)}^2}} \right] = \sum\limits_x {{{\left( {X – {\rm{E}}\left[ X \right]} \right)}^2}{p_X}\left( x \right)} = {\rm{E}}\left[ {{X^2}} \right] – {\left( {{\rm{E}}\left[ X \right]} \right)^2}\]

\begin{align*}
{\rm var} \left[ {\alpha X + \beta } \right] &= {\alpha ^2}{\mathop{\rm var}} \left( X \right)\\
{\rm{independent}} \to {\rm var} \left( {X + Y} \right) &= {\rm var} \left( X \right) + {\mathop{\rm var}} \left( Y \right)
\end{align*}

Standard deviation: \[{\sigma _X} = \sqrt {{\rm var} \left( X \right)} \]

Continuous random variables

PDF: probability density function \({f_X}\)

\begin{align*}
{\rm{P}}\left( {a \le X \le b} \right) &= \int_a^b {{f_X}\left( x \right)dx} \\
{\rm{P}}\left( {\left( {X,Y} \right) \in S} \right) &= \int {\int {{f_{X,Y}}\left( {x,y} \right)dxdy} }
\end{align*}

\begin{align*}
Y = aX + b &\to {f_Y}\left( y \right) = \frac{1}{{\left| a \right|}}{f_X}\left( {\frac{{y – b}}{a}} \right)\\
{f_{X,Y}}\left( {x,y} \right) &= {f_X}\left( x \right){f_{Y\left| X \right.}}\left( {y\left| x \right.} \right) = {f_Y}\left( y \right){f_{X\left| Y \right.}}\left( {x\left| y \right.} \right)\\
{f_Y}\left( y \right) &= \int_x {{f_X}\left( x \right){f_{Y\left| X \right.}}\left( {y\left| x \right.} \right)dx} \\
{f_{X\left| Y \right.}}\left( {x\left| y \right.} \right) &= \frac{{{f_{X,Y}}\left( {x,y} \right)}}{{{f_Y}\left( y \right)}} = \frac{{{f_X}\left( x \right){f_{Y\left| X \right.}}\left( {y\left| x \right.} \right)}}{{{f_Y}\left( y \right)}}
\end{align*}

\begin{align*}
{\rm{independent}} \to {f_{X,Y}}\left( {x,y} \right) &= {f_X}\left( x \right){f_Y}\left( y \right)\\
{f_{X\left| Y \right.}}\left( {x\left| y \right.} \right) &= {f_X}\left( x \right)
\end{align*}

CDF: cumulative distribution function \({F_X}\)

\[{F_X}\left( x \right) = {\rm{P}}\left( {X \le x} \right) = \int_{ – \infty }^x {{f_X}\left( t \right)dt} \]

\begin{align*}
{\rm{E}}\left[ X \right] &= \int_{ – \infty }^\infty {{f_X}\left( x \right)dx} \\
{\rm{E}}\left[ {g\left( X \right)} \right] &= \int_{ – \infty }^\infty {g\left( x \right){f_X}\left( x \right)dx} \\
{\rm{E}}\left[ {g\left( {X,Y} \right)} \right] &= \int_{ – \infty }^\infty {\int_{ – \infty }^\infty {g\left( {x,y} \right){f_{X,Y}}\left( {x,y} \right)dxdy} } \\
{\rm{independent}} \to {\rm{E}}\left[ {XY} \right] &= {\rm{E}}\left[ X \right]{\rm{E}}\left[ Y \right]\\
{\mathop{\rm var}} \left( X \right) &= \int_{ – \infty }^\infty {{{\left( {x – {\rm{E}}\left[ X \right]} \right)}^2}{f_X}\left( x \right)dx}
\end{align*}

Gaussian PDF = normal PDF

\begin{align*}
{\rm{standard \ normal \ }}N\left( {0,1} \right) \ &{f_X}\left( x \right) = \frac{1}{{\sqrt {2 \pi }}}{e^{ – {x^2}/2}}\\
{\rm{general \ normal \ }}N\left( {\mu ,\sigma ^2} \right) \ &{f_X}\left( x \right) = \frac{1}{{\sigma \sqrt {2 \pi} }}{e^{ – {{\left( {x – \mu } \right)}^2}/2{\sigma ^2}}}
\end{align*}

\begin{align*}
{\rm{E}}\left[ X \right] &= \mu ,{\mathop{\rm var}} \left( X \right) = {\sigma ^2}\\
Y = aX + b &\to Y \sim N\left( {a\mu + b,{a^2}{\sigma ^2}} \right)
\end{align*}

\[X \sim N\left( {\mu ,{\sigma ^2}} \right) \to {\rm{P}}\left( {X \le a} \right) = {\rm{P}}\left( {\frac{{X – \mu }}{\sigma } \le \frac{{a – \mu }}{\sigma }} \right) = CDF\left( {\frac{{a – \mu }}{\sigma }} \right)\]

Derived distribution 

#1 \({f_{X,Y}}\left( {x,y} \right),g\left( {X,Y} \right)\)

\begin{align*}
{\rm{E}}\left[ {g\left( {X,Y} \right)} \right] &= \int {\int {g\left( {x,y} \right){f_{X,Y}}\left( {x,y} \right)dxdy} } \\
{F_Y}\left( y \right) = {\rm{P}}\left( {Y \le y} \right) &\to {f_Y}\left( y \right) = \frac{{d{F_Y}}}{{dy}}\left( y \right)
\end{align*}

#2 \(Y = g\left( X \right)\), \(g\) is strictly monotonic

\begin{align*}
x \le X \le x + \delta &\Leftrightarrow g\left( x \right) \le Y \le g\left( {x + \delta } \right) \approx g\left( x \right) + \delta \left| {\frac{{dg}}{{dx}}\left( x \right)} \right|\\
\delta {f_X}\left( x \right) &= \delta {f_Y}\left( y \right)\delta \left| {\frac{{dg}}{{dx}}\left( x \right)} \right|
\end{align*}

Example 1 \({f_{X,Y}}\left( {x,y} \right) = 1\) figured as follow, and \(Z = \frac{Y}{X} = g\left( {X,Y} \right)\).

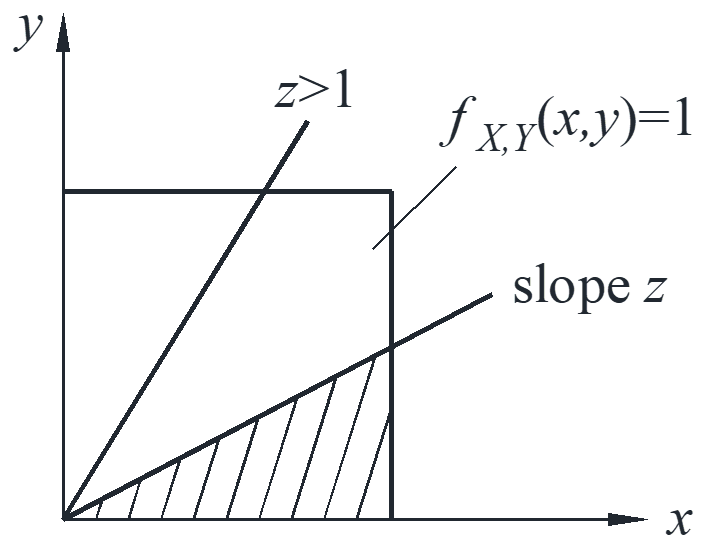
\[{F_Z}\left( z \right) = \left\{ \begin{array}{l}
{\rm{P}}\left( {\frac{Y}{X} \le 1} \right) = \frac{z}{2},0 \le z \le 1\\
{\rm{P}}\left( {\frac{Y}{X} \ge 1} \right) = 1 – \frac{1}{{2z}},z \ge 1
\end{array} \right. \to {f_Z}\left( z \right) = \left\{ \begin{array}{l}
\frac{1}{2},0 \le z \le 1\\
\frac{1}{{2{z^2}}},z \ge 1
\end{array} \right.\]

\[{\rm{E}}\left[ Z \right] = \int_0^1 {z\frac{1}{z}dz} + \int_1^\infty {z\frac{1}{{2{z^2}}}dz} = 1 + \infty \]

\begin{align*}
{\rm{E}}\left[ Z \right] &= \frac{{{\rm{E}}\left[ Y \right]}}{{{\rm{E}}\left[ X \right]}} \quad {\rm{only \ true \ for \ linear \ function}}\\
&= {\rm{E}}\left[ X \right]{\rm{E}}\left[ {\frac{Y}{X}} \right] \quad {\rm{X,Y \ are \ independent}}
\end{align*}

Example 2 \(Y = {X^3}\), \(X\) is uniformly distributed on \([0,2]\), what is PDF of \(Y\)?

method 1:

\begin{align*}
y &= g\left( x \right) = {x^3},x = {y^{1/3}}\\
{f_X}\left( x \right) &= {f_Y}\left( y \right)\frac{{dg\left( x \right)}}{{dx}} = {f_Y}\left( y \right) \cdot 3{x^2}\\
{f_Y}\left( y \right) &= \frac{{{f_X}\left( x \right)}}{{3{x^2}}} = \frac{{{f_X}\left( {{y^{1/3}}} \right)}}{{3{y^{2/3}}}} = \frac{1}{2} \cdot \frac{1}{{3{y^{2/3}}}} = \frac{1}{6}{y^{ – 2/3}}
\end{align*}

method 2: accumulation

\begin{align*}
{F_Y}\left( y \right) &= {\rm{P}}\left( {Y \le y} \right) = {\rm{P}}\left( {{x^3} \le y} \right) = {\rm{P}}\left( {x \le {y^{1/3}}} \right) = \frac{1}{2}{y^{1/3}}\\
{f_Y}\left( y \right) &= \frac{{d{F_Y}\left( y \right)}}{{dy}} = \frac{1}{6}{y^{ – 2/3}}
\end{align*}

Corvariance

\[{\mathop{\rm cov}} \left( {X,Y} \right) = {\rm{E}}\left[ {\left( {X – {\rm{E}}\left[ X \right]} \right) \cdot \left( {Y – {\rm{E}}\left[ Y \right]} \right)} \right] = {\rm{E}}\left[ {XY} \right] – {\rm{E}}\left[ X \right]{\rm{E}}\left[ Y \right]\]

\begin{align*}
{\mathop{\rm cov}} \left( {X,X} \right) &= {\rm{E}}\left[ {{{\left( {X – {\rm{E}}\left[ X \right]} \right)}^2}} \right] = {\mathop{\rm var}} \left( X \right)\\
{\rm{zero-mean \ case}} \quad &{\rm{cov}} \left( {X,Y} \right) = {\rm{E}}\left[ {XY} \right]
\end{align*}

\[\rho = {\rm{E}}\left[ {\frac{{\left( {X – {\rm{E}}\left[ X \right]} \right)}}{{{\sigma _X}}} \cdot \frac{{\left( {Y – {\rm{E}}\left[ Y \right]} \right)}}{{{\sigma _Y}}}} \right] = \frac{{{\mathop{\rm cov}} \left( {X,Y} \right)}}{{{\sigma _X}{\sigma _Y}}}, – 1 \le \rho \le 1\]

\begin{align*}
\left| \rho \right| = 1 \Leftrightarrow \left( {X – {\rm{E}}\left[ X \right]} \right) = c\left( {Y – {\rm{E}}\left[ Y \right]} \right) \quad &{\rm{linear \ related}}\\
{\rm{independent}} \to \rho = 0 \quad &{\rm{converse \ is \ not \ true}}
\end{align*}

Law of iterated expectations

\[{\rm{E}}\left[ {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right] = {\rm{E}}\left[ X \right]\]

Proof:

\begin{align*}
{\rm{E}}\left[ {X\left| Y \right.} \right] &= g\left( Y \right),{\rm{E}}\left[ {X\left| {Y = y} \right.} \right] = g\left( y \right)\\
{\rm{E}}\left[ {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right] &= {\rm{E}}\left[ {g\left( y \right)} \right] = \sum\limits_y {g\left( y \right){{\rm{P}}_Y}\left( y \right)} \\
&= \sum\limits_y {{\rm{E}}\left[ {X\left| {Y = y} \right.} \right]{{\rm{P}}_Y}\left( y \right)} = {\rm{E}}\left[ X \right]
\end{align*}

Law of total variance

\[{\mathop{\rm var}} \left( X \right) = {\rm{E}}\left[ {{\mathop{\rm var}} \left( {X\left| Y \right.} \right)} \right] + {\mathop{\rm var}} \left( {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right)\]

Proof:

\begin{align*}
ar\left( X \right) &= {\rm{E}}\left[ {{X^2}} \right] – {\left( {{\rm{E}}\left[ X \right]} \right)^2}\\
{\mathop{\rm var}} \left( {X\left| Y \right.} \right) &= {\rm{E}}\left[ {{X^2}\left| Y \right.} \right] – {\left( {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right)^2}\\
{\rm{E}}\left[ {{\mathop{\rm var}} \left( {X\left| Y \right.} \right)} \right] &= {\rm{E}}\left[ {{X^2}} \right] – {\rm{E}}\left[ {{{\left( {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right)}^2}} \right]\\
{\mathop{\rm var}} \left( {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right) &= {\rm{E}}\left[ {{{\left( {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right)}^2}} \right] – {\left( {{\rm{E}}\left[ {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right]} \right)^2} = {\rm{E}}\left[ {{{\left( {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right)}^2}} \right] – {\left( {{\rm{E}}\left[ X \right]} \right)^2}\\
{\rm{E}}\left[ {{\mathop{\rm var}} \left( {X\left| Y \right.} \right)} \right] + {\mathop{\rm var}} \left( {{\rm{E}}\left[ {X\left| Y \right.} \right]} \right) &= {\rm{E}}\left[ {{X^2}} \right] – {\left( {{\rm{E}}\left[ X \right]} \right)^2} = {\mathop{\rm var}} \left( X \right)
\end{align*}