2D frame

This is a plane steel frame with box sections subjected to a point load at one node figured as below.

An dynamic implicit analysis step was defined and the following lines were added at the end of input file.

**
*STEP
*MATRIX GENERATE, STIFFNESS, MASS, LOAD, Structural Damping,Viscous Damping
*MATRIX OUTPUT, STIFFNESS, MASS, LOAD, Structural Damping,Viscous Damping, FORMAT=COORDINATE
*END STEP

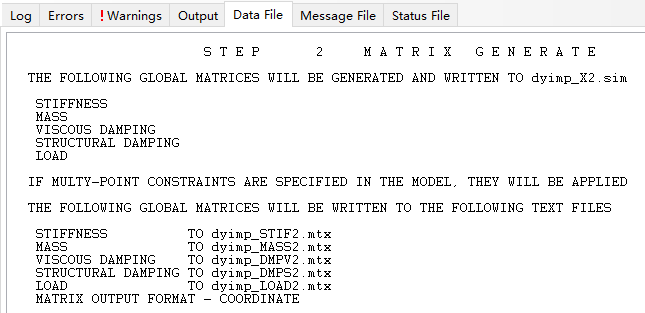
After the analysis completed, the Data file will be available and a screen shoot is provided below. The  .mtx files are generated in the file folder, however, there is no dyimp_LOAD2.mtx file and this is a problem remained. I still don’t know how to fix it.

3D frame

This is a 3D frame with rectangular sections subjected to two point loads. Firstly, the columns and beams were built, then they are assembled in ASSEMBLY section and finally I used the merge function and suppressed the original instances to form this frame. I also chose the Remove button to for the intersecting boundaries. The masses were applied on the nodes and as such the material density was set to zero. A dynamic implicit analysis case was defined and one element per member is used.

The same as the example of 2D frame, the codes were added to extract matrices from abaqus.  The matrices were written in corresponding files.

However, I found the size of matrices are not consistent with the number of nodes. There are 16 nodes in this frame and the degree of freedom is 16*6=96, but the size of matrices are 144*144 and this is puzzling. To find out the reason of this, I re-extracted the matrices in coordinate form and defined a frequency step to output the element matrices. Also, I checked the numbers of nodes and elements in MESH section as follow.

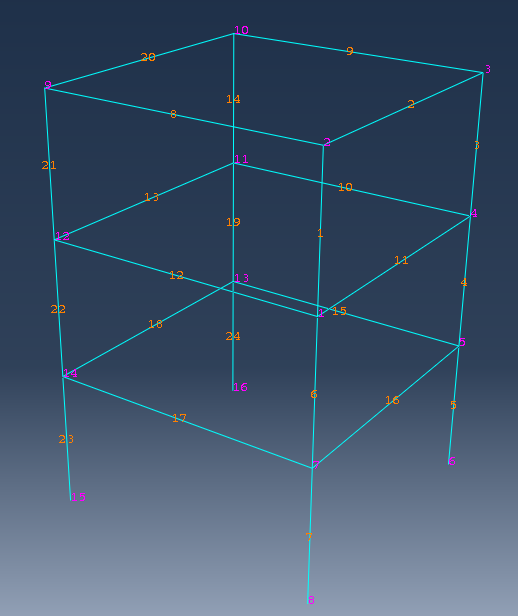
From the numbers in MESH section, there is no error in it. The matrices in Coordinate form show that both the row and column labels have negative values. The numbers are from -24 to +16 and the negative part is very confusing. The 24 negative numbers are the geometrical nodes (3*4*2) as I understand. However, why these degree of freedoms are not condensed is unknown, probably there is no defined restrains in INTERACTION section. The element matrices file shows there are totally 24 elements in the model and this result correspond with the structure.

From these results, it can be concluded that the negative numbers are from the assembling of global matrices. I guess this may result from the merge of beams and columns. Thus, I built another frame with Tie constrains on the nodes at the same position. The numbers in MESH section is illustrated as below.

It can be seen that every column has 4 nodes and every beam has 2, the sum is 40 nodes. In the matrices in coordinate form, the number of nodes is from 1 to 40, corresponding to total number of nodes. In the matrices in matrix input form, the maximum number of row and column labels is 96, equals to 16*6, meaning the nodes at the same position are condensed to one in global matrix because of the Tie constrains.

One more question, the matrix in matrix input form has more non-zero elements (1504) than matrix in coordinate form (800).  This condition also exsists in the last model in this example and 2D frame example (12 nodes, 828 elements for coordinate form and 450 elements for matrix input form). In this example, there are 16 nodes after the condensation of degree of freedoms, so there will be 16*6=96 rows and lines, that is 96*96=9216 elements in the matrix. The number of non-zero elements in matrix in coordinate form except the diagonal part is 1504-96=1408. Half of the non-zero elements except the diagonal (1480/2=704) plus the the diagonal part (96) is the number of elements in  matrix in matrix input form. The conclusion is that the matrix in matrix input form omits the symmetrical part of elements as you can fill in them according to the symmetry principle with the node numbers and degree of freedom numbers.

The six degree of freedoms of nodes 25, 29, 33, 37 (four button nodes) are set to be a very large value 1.0E+36 in stiffness matrix in  matrix input form, and the value of row and column labels 1~6, 25~30, 49~54, 73~78 are also 1.0E+36 in stiffness matrix in  coordinate form. The assembling of global is not according to the sequence of node numbers.

Up to now, I haven’t found any explanations in official support documents about the negative node number. If you want to extract the matrices from abaqus and use them in other software, you’d better establish the model in the second way in this example I think.

Updated 2018/8/24

Exporting the load vectors

Section 10.3.1 in Abaqus Analysis User’s Guide

All types of loads can be applied in the load cases for a matrix generation step. Real and imaginary parts of the load vectors will be generated for the complex loads. Any loads that are defined in a matrix generation step will not be used in subsequent general analysis steps (unless they are respecified).

So, in the matrix generation step, we need to define the load again and the load matrix can be exported to .mtx file. The codes for exporting matrices in input file is described below.

*STEP
*MATRIX GENERATE, STIFFNESS, MASS, LOAD, Structural Damping,Viscous Damping
*MATRIX OUTPUT, STIFFNESS, MASS, LOAD, Structural Damping,Viscous Damping, FORMAT=COORDINATE
** LOADS
**
** Name: Load-1 Type: Concentrated force
*Cload, amplitude=Amp-1
_PickedSet79, 1, 100.
**
**
*END STEP

The vector in LOAD.mxt file is listed as

** Assembled nodal loads
*CLOAD, REAL
19 9.999999999999999e-35
67 9.999999999999999e-35

Updated 2019/01/06

Negative values in row and column labels in matrix

I found the reason for negative values in row and column labels in matrix yesterday and tried to check this out this morning. The reason for this phenomenon lies on the method of merge. Three methods, geometry, mesh and both, are included in ABAQUS, as shown below. 

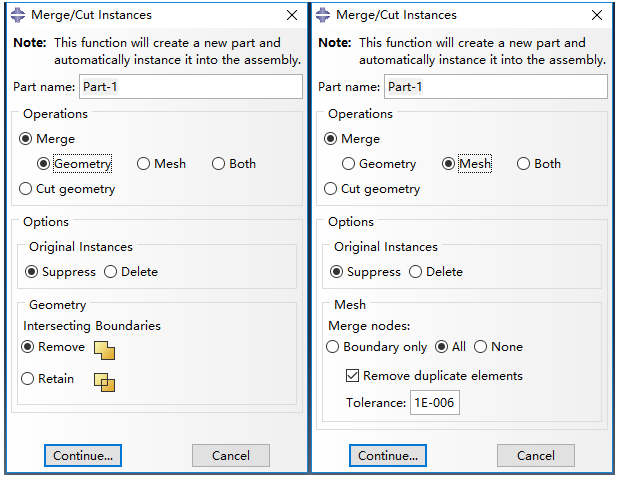
In the first method, Geometry, only the intersecting boundaries are removed and the duplicate nodes are also removed. In the second method, Mesh, the duplicated elements as well as the nodes can be removed. A prompt message will emerge “The nodes highlighted in magenta will be merged. OK to merge?” The matrix exacted by this method do not contain row and column labels with negative values. 

Since I cannot find the original model and codes, I tried to merge the model with the two methods and found the matrix of them do not contain negative values either. The negative value I got before might be the result of forgetting to choose Remove intersecting boundaries.

To sum up, if you do not want to have negative rows and columns, you can use INTERACTION (such as tie, MPC) to deal with the nodes of elements or you can merge with Geometry or Mesh and remember to choose to remove the duplicate nodes. When you merge with Geometry and retain the intersecting boundaries, negative values will be generated in the matrix.